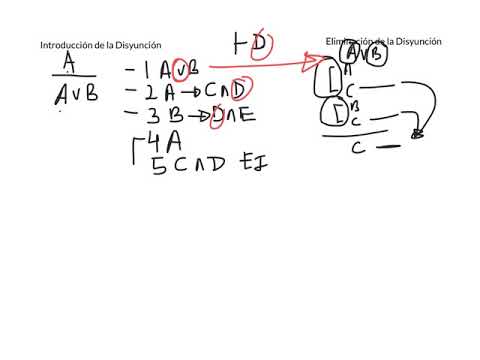
Introducción de la disyunción

Introducción de la disyunción o adición es una simple forma de argumento válido, una inferencia inmediata y una regla de inferencia de la lógica proposicional.^[1]​^[2]​^[3]​ La regla hace posible la introducción de disyunciones de pruebas lógicas. Es la inferencia de que si P es verdad, entonces P o Q tiene que ser verdad.

A modo de ejemplo:

Sócrates es un hombre.

Por lo tanto, o bien Sócrates es un hombre o unos cerdos están volando en formación sobre el canal inglés.

La regla se puede expresar como:

${\displaystyle {\frac {P}{\therefore P\lor Q}}}$

donde la regla es que cada vez que aparecen las instancias de ${\displaystyle P}$ en las líneas de se puede colocar en una prueba, ${\displaystyle P\lor Q}$ en una línea posterior.

En la lógica paraconsistente, la introducción de la disyunción es controversial porque, en combinación con otras reglas de la lógica, conduce a la explosión: todo se vuelve demostrable (véase compensaciones en la lógica paraconsistente).

Notación formal

La regla de introducción de la disyunción puede escribirse en la notación subsiguiente:

${\displaystyle P\vdash (P\lor Q)}$

donde ${\displaystyle \vdash }$ es un símbolo metalógico que significa que ${\displaystyle P\lor Q}$ es una consecuencia sintáctica de ${\displaystyle P}$ en algún sistema lógico;

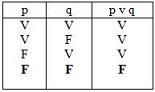
y se expresa como una tautología funcional verdadera o teorema de la lógica proposicional:

${\displaystyle P\to (P\lor Q)}$

donde ${\displaystyle P}$ y ${\displaystyle Q}$ son proposiciones expresadas en algún sistema formal.

Referencias

Enlaces externos